The following study came out of wondering whether the Exodus Hebrew Calendar intercalation pattern, presented in my previous article “In Search of the Original Hebrew Calendar,” would conflict with my 2018 study on the date of Christ’s birth.
Updating the Priestly Divisions Spreadsheet
A new version of the “Priestly Divisions, 70 AD–8 BC” Excel spreadsheet has been created, an update of the original 2018 version. The key difference is that a column for the Exodus Hebrew Calendar has been added. In my original “Pinpointing the Date of Christ’s Birth” article, the Hebrew dates in the priestly service table were taken from the Hebrew / Roman Calendar Comparison on the Church of God Study Forum (CGSF) website; for example, HERE is the CGSF calendar for AD 70. The intercalations (leap years) determined in the Exodus Hebrew Calendar research differ from those of the CGSF in certain years, leading to differences from the CGSF data of up to a month. It was discovered, though, that none of these changes impacted the analysis of the birth of Christ; the important periods of the two calendars happen to be in agreement.
In fact, in some ways the Exodus Hebrew Calendar is an improvement on the CGSF calendar for figuring out the date of Christ’s birth. Here is a section of the revised chart for AD 70:
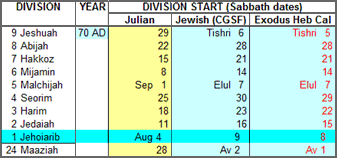
Jewish dates begin around 6 pm the day before the Julian date it is customarily “pegged” to by today’s standard daylight-based date assignment method. For instance, on August 4, 70 AD, the CGSF Jewish date pegged to it – Av 9 – actually began at sunset the previous day, August 3, and continued until 6 pm on August 4, when it changed to Av 10. For the Exodus Hebrew Calendar column, Jewish dates were determined using the Parker and Dubberstein (P&D) Babylonian date calculator at https://webspace.science.uu.nl/~gent0113/babylon/babycal_converter.htm. That calculator pegs the Jewish date for August 4 one day earlier than the CGSF tables, Av 8 rather than Av 9. All of the dates given in the above chart are Saturday Sabbath dates. This means that the Exodus Hebrew Calendar pegs Av 9 to the next day, Sunday.
This calendar difference might be considered trivial, but it has some significance in view of what the Seder ‘Olam Rabbah reports (ch. 30). As quoted in the Milikovsky translation at https://www.thetorah.com/article/tisha-b-av-on-what-day-were-the-jerusalem-temples-destroyed:
“When the First Temple was destroyed, it was the night after Shabbat, and it was the year after a Sabbatical year, and it was the service time of the Yehoyariv family, and it was the 9th of Av. The same is true of the Second [Temple’s destruction].”
The author of that article then observes,
The point here is that not only did the dates match, but even the day of the week, the place of the year in the seven-year cycle, and the priestly family doing the service in the Temple for that week matched.
We can see the new determination based on the Exodus Hebrew Calendar, by putting the Sabbath on Av 8, puts the 9th of Av on “the night after Shabbat.” That began at sunset on Av 8. The family of Jehoiarib started its service at midday on Av 8, so they were in charge on the 9th when the destruction took place. This date is apparently in conflict with what Scripture reports about the destruction of the First Temple, as discussed under “Biblical Depictions of the Destruction of the First Temple” at https://www.thetorah.com/article/tisha-b-av-on-what-day-were-the-jerusalem-temples-destroyed (2 Kgs 25:10–12 and Jer 52:12–14). This difference can be explained by the Jewish leaders desiring to seek synchrony between the destruction of the Second Temple, which they had accurate knowledge of, and the first. They thus chose to follow their tradition rather than the Scriptures, a penchant the Lord Jesus condemned in no uncertain terms:
Then the LORD said,
“Because this people draw near with their words
And honor Me with their lip service,
But they remove their hearts far from Me,
And their reverence for Me consists of tradition learned by rote,
Therefore behold, I will once again deal marvelously with this people, wondrously marvelous;
And the wisdom of their wise men will perish,
And the discernment of their discerning men will be concealed.”
– Isaiah 29:13–14
After quoting the above passage, Jesus followed up with these words:
“Hear and understand. It is not what enters into the mouth that defiles the man, but what proceeds out of the mouth, this defiles the man.” Then the disciples came and said to Him, “Do You know that the Pharisees were offended when they heard this statement?” But He answered and said, “Every plant which My heavenly Father did not plant shall be uprooted. Let them alone; they are blind guides of the blind. And if a blind man guides a blind man, both will fall into a pit.”
– Matthew 15:10–14
(See also my comments under “Were Both Temple Destructions in Sabbatical Years?” at https://biblearchaeology.org/abr-projects-main/the-daniel-9-24-27-project-2/4590-the-going-forth-of-artaxerxes-decree-part2. This is a caution to us all to exercise discernment in how much stock we place in Talmudic pronouncements.)
To summarize, the new data in the Exodus Hebrew Calendar intercalation pattern perfectly matches up with the starting point for counting back the priestly divisions to get to that of Abijah in 7 BC, when Zacharias was serving in the Temple (Luke 1:5–25). From this point the date of the birth of Jesus follows.
Making an Exception in 6 BC
In creating the Exodus Hebrew Calendar, I made the conscious decision not to try to analyze crescent moon observation studies – such as those of Schaefer and Hoffman, mentioned in the last article – to judge when it was likely that the moon was observed a day earlier at Jerusalem than at Babylon. I made the simplifying assumption that in the vast majority of cases, the two locations were close enough geographically that there would have been no difference in the crescent observation that started a month; and if there was, adherence to the same intercalation pattern (to keep the months the same during the exile) would have brought the calendars back to agreement quickly. I was thus generally content to allow the Babylonian data to set the first days of months for the Jews as well.
There was one notable exception to this approach, however, that I felt uncomfortable with: the determination of the date of Christ’s birth. As my “Pinpointing the Date of Christ’s Birth” article pointed out, the research of astronomer Michael Molnar set the Magi’s date for the astrologically-significant occultation of Jupiter by the moon in Aries as March 20 on the Julian calendar. When I used the Hebrew calendar from CGSF for 6 BC, I was thrilled to find that it pegged Nisan 1 to Saturday, March 20. That was so shocking, I stopped my analysis right there and accepted it as given. In retrospect, I erred by not digging deeper.
Digging Deeper
The development of the Exodus Hebrew Calendar gave a reason to do the necessary deeper investigation. I belatedly realized that according to the CGSF data, the sunset which initiated Nisan 1 was that of March 19, making Molnar’s sunset on March 20 the start of Nisan 2. As for the Exodus Hebrew Calendar, its default use of Babylonian – not necessarily Jewish – first days of months pegged Nisan 1 to March 22, so Nisan 1 began after sunset on March 21. Thus, neither of these worked perfectly with the idea that the birth of Christ was after sunset on March 20. Of course, we might simply shelve the whole idea of drawing a type/antitype comparison between the completed physical body of the newborn Jesus and completion of the mishkan Tabernacle on Nisan 1, but the comparison seems worth defending. Was there a way to resolve this apparent difficulty?
The basis for Molnar’s March 20 date was his determination that this was an important date astrologically for the Magi. As discussed in “Pinpointing the Date of Christ’s Birth,” they could not have determined this from observation, for in the environs of Babylon the occultation in the evening of March 20 was too low on the horizon to be visible. They could only have detected it from their knowledge of astronomical orbital geometry which the Greeks had previously developed and spread through Alexander’s former empire. It was thus a calculated occultation of Jupiter by the moon which the Magi detected. This leads to the suspicion that in the same way, instead of using the Babylonian observed crescent date given in P&D to mark the start of the spring lunation in 6 BC, calculated astronomical data played an important role, as did the 19-year intercalation cycle uncovered in “In Search of the Original Hebrew Calendar.”
The Astropixels website says the astronomical New Moon of Nisan in 6 BC was on March 19 at 21:28 UTC. When 2:21 is added to the UTC time to convert it to local Jerusalem time, this made it 11:49 pm, well after sunset and thus unseen. Nevertheless, the science of the day would have told the Jewish leaders the conjunction took place on the 19th, so they would have known to look for the first manifestation of the Nisan lunation shortly after sunset the following day, March 20.
The Sanhedrin, also called the Beis Din Hagadol (“the great house of law”), was the final arbiter of when to declare the start of a new month. Drawing mainly from the Jewish sage Maimonides, also known as Rambam, at https://www.shulchanaruchharav.com/wp-content/uploads/wp-post-to-pdf-enhanced-cache/1/the-process-of-determining-rosh-chodesh-in-times-of-the-sanhedrin.pdf the Halacha Knowledge Base notes:
Who determines Rosh Chodesh [the first day of the month] based on visibility of the moon? Although we explained above that Rosh Chodesh is determined by the moon’s visibility, nonetheless, this determination was not given into the hands of the individual viewer but rather to the Beis Din (emphasis added). Beis Din would first have to calculate as to whether it is possible for the new moon to be seen on the 30th day, and then collect testimony from witnesses who viewed the moon. After corroboration of the testimony, the Beis Din would have to declare on the 30th day that it is Rosh Chodesh. If for whatever reason Beis Din did not make this declaration, the month remains a 30-day month and Rosh Chodesh only begins the next day on the 31st day of the month.
In theory, then, only two sharp-eyed eyewitnesses were necessary to set the previous month at 29 days, otherwise that month was 30 days long whether or not eyewitnesses came forth. But there were exceptions – and these were based not on Scripture, but on the preferences of the Jewish leaders. The article continues:
Calculating the new moon? Even in the times of testimony, part of the Biblical command to sanctify the new month included that the Beis Din was required to calculate as to when the new moon would become potentially visible. If the moon would not be visible on the 30th day, based on their calculations, then the Beis Din would not accept testimony and any potential witnesses would be automatically disqualified as false or in error of what that which [sic] they saw. Rosh Chodesh would automatically be set for the 31st day. If Beis Din calculated that the new moon could be seen on the 30th day, then they would await witnesses to testify and be properly interrogated, corroborating their testimony. At times, despite the calculations, the moon is not visible due to clouds and position, and therefore the Beis Din must wait and see if in truth the moon was seen or not. We will now explore a case in which the new month on the 30th was determined based only on calculation and not on witnesses even in the times of the Sanhedrin.
Relying only on calculation – What was done in the event that witnesses did not come forward month after month? In the event that the moon was not seen for one month after the other, such as due to clouds or positioning, and hence no witnesses came forward, the future months are set not in accordance to testimony of the moon’s visibility but rather in accordance to calculation, having one month Malei [“full,” 30 days] and one month Chaseir [“missing,” 29 days], or two months Malei or two months Chaseir, in accordance to the calculation. The reason why this is done is because if the Beis Din would make every month Malei due to lack of testimony, then it would end up that after 10 months the new moon begins to appear 5-6 days before Rosh Chodesh, and there is no greater matter of ridicule than this, and it destroys the whole concept of basing the new month on the new moon. Thus, in conclusion we see that at times, even during the era of the Sanhedrin when the new month was sanctified based on testimony, they would have to set the new month based solely on calculation and negate testimony in order to prevent a catastrophic misalignment between the new moon and the new month. This matter was a tradition of Moshe from Sinai, that at times the Beis Din must forgo the testimony and rely solely on calculation. All the areas in the Talmud that mention the new month being set based on calculation alone refers to the above situation, in which the tradition applies (emphasis added).
If the above is true, it was not the word of eyewitnesses that mattered most, but the determination of the Sanhedrin. The “tradition of Moshe from Sinai” they claimed to have received apparently included the regular 19-year intercalation pattern that the Babylonians eventually also embraced.
As reflected in the calculated calendar of Hillel II, the Jewish calendar has the twelfth month, Adar, fixed at 29 days; see https://www.chabad.org/library/article_cdo/aid/526874/jewish/The-Jewish-Month.htm. If the thin crescent moon was not observed the evening that began the thirtieth day, the month was reckoned as 30 days long, triggering the intercalation of an extra month. Hillel II's 30-day Adar intercalation trigger was apparently not created in a vacuum but reflected prior Jewish practice, though it is unclear when this approach to intercalation became standardized. P&D’s records reflect that many Babylonian years were intercalated despite having only 29 days in Addaru (for instance, in 13, 5 and 2 BC, and 18, 23, 26 and 32 AD – see the Exodus Jewish Calendar), so Jewish practice in this regard, as with not intercalating a second Elul, seems to have reflected a divergence from Babylonian customs. It was likely linked to Babylonian insistence on not starting Nisan until on or after the vernal equinox.
With this in mind, it stands to reason that if Adar in 6 BC had to have 29 days to conform with the 19-year intercalation cycles and presumably the ripeness of the barley harvest, the Sanhedrin would have decided of their own initiative to make it a Chaseir month, rather than allow a lack of eyewitness reports to make it Malei and result in adding an extra month to the year. According to the CGSF, Murphey, and the Exodus Hebrew Calendar, the Jewish calendar that overlapped with 7 BC included a thirteenth month that made it intercalated. Since there were never two intercalated years in a row, this strongly implies the Sanhedrin would not have allowed Adar in 6 BC to be a 30-day month requiring an added 29-day Adar-II. It would have disrupted the settled 19-year intercalation pattern which allowed the Jewish and Babylonian calendars to essentially match during the exile and thereafter (Zec 1:7, 7:1; Est 2:16, 3:7, 3:13, 8:9, 8:12, 9:1).
Insights from Sacha Stern
After the Maccabees removed the Seleucids from power and the Hasmonean Era began, the role of the Sanhedrin became increasingly influential. As ancient calendar expert Sacha Stern writes in Calendar and Community (Oxford, 2001):
Whether the Judaean calendar of the Hasmonaean period corresponded exactly to the Babylonian reckoning cannot be known. Hasmonaean rulers are more likely to have set their own calendar independently than to have relied on moon sightings and declarations of new moons that were being made in Babylonia, a region that was now part of a foreign kingdom. Still, the methods employed by the Hasmonaeans to determine lunar months were probably similar to those of the Babylonians (p. 30).
He adds on p. 31:
It is also questionable whether the Hasmonaeans made the same intercalations as in the Babylonian calendar, thus always celebrating Passover in the Babylonian Nisan – as had been the practice in the Persian period (e.g. at Elephantine). Datings from the Hasmonaean and early Roman periods… suggest that Jewish and Babylonian months regularly coincided. However, this evidence is too sporadic to prove that the Babylonian calendar was consistently followed and used… This [Babylonian] cycle may have been considered unsuitable to the Jews for a number of other reasons. Firstly, the intercalation of a second month of Ululu (Elul) in the 17th year of the Babylonian cycle may not have been acceptable to the Jews, for whom the subsequent month of Tishre had to correspond, every year, to the biblical 7th month: if an additional Elul were inserted, Tishre would have become the 8th month. To overcome this problem, a different 19-year cycle, without intercalations of Ululu, would have been needed; but then the Jewish calendar would not have been the same as the Babylonian… Nevertheless, it remains entirely possible – as the evidence indeed suggests – that the Jews of the Hasmonaean and early Roman periods relied to a large degree on the Babylonian cycle of intercalations.
This is precisely what I concluded in my previous article, when I found it necessary to assume the Jewish 19-year cycle counts began a year earlier than those of the Babylonians.
No longer tightly linked with the calendar decisions emanating from Babylon and its Seleucid successor, the Hasmonean Era saw the gradual increase in the influence of the priesthood on the Jewish calendar. This influence was manifested in some calendar manipulation to encourage late spring observance of Passover. This served to facilitate attendance at Temple activities that promoted national unity, especially the pilgrimage festivals which brought people from far and wide to Jerusalem to celebrate Passover, the Feast of Weeks, and the Feast of Booths. The efforts of Herod the Great to enlarge and embellish the Temple into a magnificent edifice also played a significant part in this.
Stern also points out (pp. 61–62):
The lateness of festivals in the first century BCE to first century CE must be attributed, therefore, to other factors… It is possible that intercalation in the Jewish calendar was based entirely, in this period, on the Babylonian system of intercalations [which kept the start of Nisan on or after the vernal equinox]… E. Schwartz has suggested that in the period of the Temple, Passover was celebrated late so as to enable pilgrims to reach Jerusalem on time for the festival. This suggestion not only is plausible in its own right, but also finds support in a rabbinic tradition that the year would be especially intercalated to allow the pilgrims already on their way to reach Jerusalem for the festival. If correct, this suggestion would explain why in subsequent centuries, after the destruction of the Temple in 70 CE, the observance of Passover appears to have receded to earlier dates in the solar year (emphasis added).
The point being made here is that these changes to the Jewish calendar during the first centuries BC and AD can be traced directly to calendar tinkering by the Jewish authorities. They diverged from the traditional, lunar observation approach to setting the start of months in favor of calculations and intervention to accomplish desired objectives. So it is fair to say that the Sanhedrin alone, with an eye to other factors besides eyewitnesses, made the final decision about what day to sanctify as the start of the month.
The Length of Adar and the Start of Nisan
In the case of determining the start of Nisan, there was an important additional factor in play not of concern with other months: if no eyewitnesses came forth the next morning to testify they had seen the crescent moon the evening that opened the thirtieth of Adar, that month was reckoned to have been 30 days long. Instead of segueing immediately to Nisan 1, an additional 29-day Adar-II had to be intercalated to the year. If this had happened in 6 BC, it would have added a second Adar rather than Nisan in March that year, resulting in Nisan 1 being postponed to April 20.
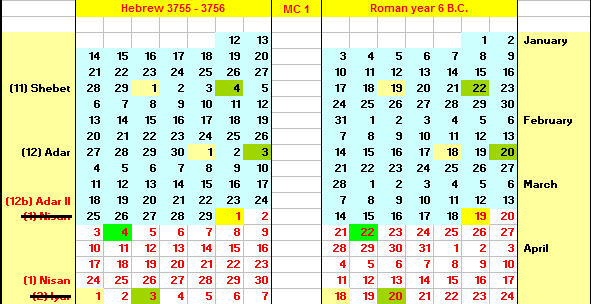
Notice that using P&D’s Babylonian data pegs Nisan 1 to March 22, even though this would make Adar a 30-day month (counting inclusively from February 20 through March 21) requiring an intercalation, indicated by the strike-throughs. Thus, March 22 should have been the start of a 29-day Adar II. But against this is the fact that the 19-year regular intercalation cycle identified for the Exodus Hebrew Calendar in the previous article expects Julian 6 BC to not include an extra Jewish month! If Adar in 6 BC was actually only 29 days long by Jewish rather than Babylonian observations, though Nisan 1 would have been “pegged” to March 21 (matching the expected intercalation pattern), it actually started at sunset on March 20. As https://www.chabad.org/library/article_cdo/aid/526873/jewish/The-Jewish-Day.htm explains:
When G‑d created time, He first created night and then day. Therefore, a Jewish calendar date begins with the night beforehand. While a day in the secular calendar begins and ends at midnight, a Jewish day goes from nightfall to nightfall. Shabbat begins on Friday night, and a yahrtzeit lamp is kindled the evening before the yahrtzeit (anniversary of a person's passing), before nightfall. If the 10th of Iyar falls on a Wednesday, and a child is born Wednesday night after dark, the child's birthday is the 11th of Iyar.
Therefore, the Jewish date pegged to any Julian date actually started at sunset about six hours earlier on the previous Julian date during the biblical period, and technically still does for the Jews, even if modern calendars do not reflect this. This is what the Exodus Hebrew Calendar would have looked like – the asterisked date is the change:
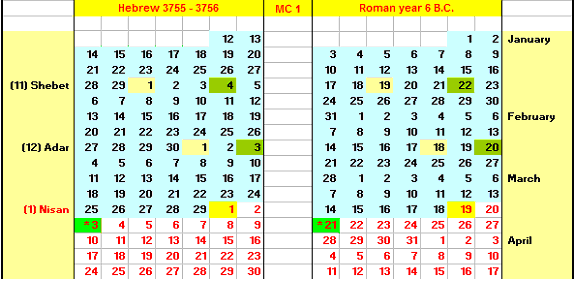
When the Exodus Hebrew Calendar is made fully “Jewish” for the first three months of 6 BC by making expected Jerusalem crescent observation dates the first days of the months instead of the astronomical New Moons, it looks like this:
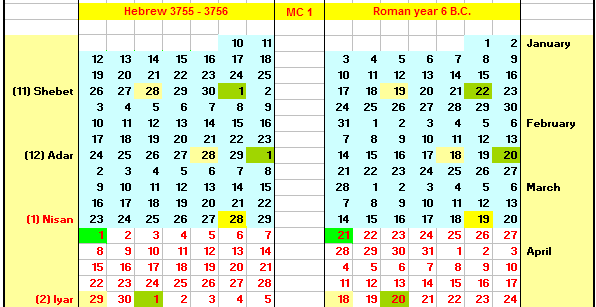
This makes it clear that the month of Adar had 29 days and was followed by Nisan, not Adar II, in 6 BC. Since the significant occultation of Jupiter by the moon took place one minute after sunset on Julian date March 20 at Jerusalem (Molnar, p. 120), that occultation took place on Jewish date Nisan 1, as the following chart indicates:
Astronomically-Determined Jewish Dates
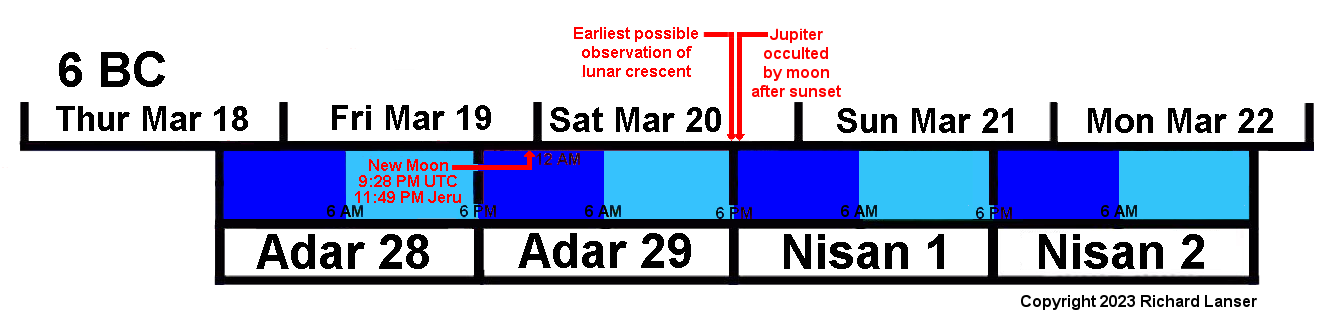
The 19-year intercalation pattern implies that the Sanhedrin would have expected eyewitnesses to have seen the crescent moon just after sunset on March 20, 6 BC. In addition, 6 BC would have marked the start of a new 19-year cycle (the “MC 1” on the calendar), providing additional motivation for the Jewish leaders to sanctify a crescent sighting on March 20, particularly if there was barley growth corroboration.
But because an observed crescent the evening of March 20 would only have been about 18.7 hours old (see below), notwithstanding that the intercalation cycle expects a 29-day Adar in 6 BC and the ultimate court of appeal was the Sanhedrin, it is fair to ask if such a young moon was potentially visible. This caused me to examine the observed lunar crescent studies of Schaefer, Yallop, Hoffman and others.
Evaluating Lunar Crescent Visibility
Five different parameters are often used to evaluate the likelihood when a thin crescent moon may first be sighted after a new moon conjunction:
• Age is the time in hours between the astronomical conjunction and the observation.
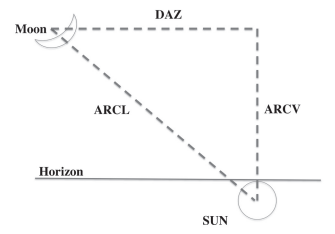
• ARCV is the altitude, the vertically-measured angle of elevation, of the moon above the sun. For a real-time observer who cannot track the sun’s location once it sinks below the horizon, it is the height of the moon above the horizon at sunset. The higher the altitude, the more likely a crescent will be spotted.
• ARCL is the elongation, the separation angle between the centers of the sun and moon. For an observer, it is the angle formed by the moon relative to the sunset point on the horizon. The greater the elongation, the better the odds a crescent will be seen.
• DAZ is the difference in azimuth between the sun and the moon. At sunset it is the horizontally-measured separation between them. As DAZ approaches 0, ARCL will decrease until it is equal to ARCV.
An illustration from Saudi astronomer Thaymer Alrefay (in The Observatory, Vol. 138, No. 1267 [December 2018], 267–291, online at https://www.researchgate.net/publication/329308491_Analysis_of_Observations_of_Earliest_visibility_of_the_lunar_crescent) helps distinguish between ARCV/altitude, ARCL/elongation, and DAZ/azimuth:
• Lag is the time difference in minutes between sunset and moonset. As the moon moves higher in the sky on succeeding nights after the conjunction, the time lag between sunset and moonset increases. A larger lag implies greater visibility of a crescent moon, for the sun goes deeper below the horizon and the sky is darker, so the moon has greater contrast. This means a more easily visible crescent.
A Close Look at the Data: Stellarium
With this background, let us examine the pertinent data for March 20 and 21 in 6 BC, as reported by the free astronomy program Stellarium (downloadable from https://stellarium.org/):

From the conjunction at 11:49 pm on March 19 to the time of best visibility on March 20 (6:31 pm according to the LunaCal program, see below) was 18 hours and 42 minutes, making the moon’s age 18.7 hr (0.8 days). Sunset at Jerusalem on March 20 occurred at 6:10 pm and moonset at 6:50 pm, a lag of 40 minutes. At the time of best visibility, when the sky had dimmed slightly and the crescent contrasted better, the sun’s altitude was 5.3° below the horizon and the moon’s 2.6° above it, so the relative altitude (ARCV) was 7.9°; elongation (ARCL) was 8.0°, and the azimuth difference between the sun and moon (DAZ) was 2.4°. As for March 21, the moon’s age was 1.6 days (38.4 hr) with lag 95 minutes, ARCV 18.9°, ARCL 19.0°, and DAZ 3.0°. Do these statistics allow for a sighting of the crescent the evening of March 20?
The United States Naval Observatory
The USNO presents at https://aa.usno.navy.mil/faq/crescent a very helpful page devoted to discussing crescent moon visibility generally. It notes:
Although the date and time of each New Moon can be computed exactly, the visibility of the lunar crescent as a function of the Moon’s “age” – the time counted from New Moon – depends upon many factors and cannot be predicted with certainty. During the first two days after New Moon, the young crescent Moon appears very low in the western sky after sunset, must be viewed through bright twilight, and sets shortly after sunset. The sighting of the lunar crescent within one day of New Moon is usually difficult. The crescent at this time is quite thin, has a low surface brightness, and can easily be lost in the twilight. Generally, the lunar crescent will become visible to suitably-located, experienced observers with good sky conditions about one day after New Moon. However, the time that the crescent actually becomes visible varies quite a bit from one month to another. Naked-eye sightings as early as 15.5 hours after New Moon [0.6 day] have been reliably reported while observers with telescopes have made reliable reports as early as 12.1 hours after New Moon. Because these observations are exceptional, crescent sightings this early in the lunar month should not be expected as the norm (emphasis and bracketed notes added).
The USNO report thus allows for the possibility of the sighting of an 18.7 hr lunar crescent, and definitely one 1.6 days (38.4 hr) old, weather permitting. It also adds,
The visibility of the young lunar crescent depends on sky conditions and the location, experience, and preparation of the observer. Generally, low-latitude and high-altitude observers who know exactly where and when to look will be favored. For observers at mid-northern latitudes, months near the spring equinox are also favored, because the ecliptic makes a relatively steep angle to the western horizon during these months. The steep angle means the Moon's altitude will be greater just after sunset (emphasis added).
The emphasized words are pertinent to Molnar’s March 20 date, because both Babylon and Jerusalem are in the mid-northern latitudes and this date was just before the spring equinox.
Data from Schaefer
In L. Doggett and Bradley E. Schaefer, “Lunar Crescent Visibility” (Icarus 107 [1994], 388–403), Table IV on p. 393 reports observed crescent moons from a series of “Moonwatches,” the last being on May 5, 1989. Summarizing their observations, they reported on p. 402:
Previously, the youngest Moon ever seen with unaided vision was 15.4 hr by J. Schmidt; with optical aid [binoculars or telescope] the record was 14.9 hr by R. Moran (Schaefer 1988b). The record for observations with optical aid was broken by several groups during Moonwatch 4, with the new record being 13.4 hr by R. Victor (Table IV, observation 239). We note that the naked-eye sighting by S. O’Meara (Table IV, observation 252), at an age of 15.5 hr, is very close to Schmidt’s record.
Schaefer subsequently wrote (“Lunar Crescent Visibility,” https://articles.adsabs.harvard.edu/pdf/1996QJRAS..37..759S) that the Schmidt sighting had been discredited. The current record was set by John Pierce on February 25, 1990, who made a well-documented naked eye sighting of a 15.0 hr lunar crescent in eastern Tennessee. Another researcher, James Stamm, set the record for a telescope-assisted observation with a 12.1 hr sighting on January 21, 1996 at Tucson, Arizona. At https://www.astronomycenter.net/record.html?l=en can be found these details about the very early unassisted observation made by Pierce:
• Longitude: 83.5 W
• Latitude: 35.6 N
• Elevation: 1500 m
• Conjunction: 25 February 1990, at 08:54 UT
• First Visibility: 25 February 1990, at 23:55 UT
• Age (at First Visibility): 15 hours and 01 minute [18.7 hr]
• Lag time: 39 minutes [40 m]
• Elongation (ARCL at Best Time): 7.6° [8.0°]
• Relative Azimuth (DAZ at Best Time): 0.6° [2.4°]
• Relative Altitude (ARCV at Best Time): 7.6° [7.9°]
Those values are all less than or equal to those from Stellarium in brackets. They indicate that in principle, the lunar crescent on March 20, 6 BC could have been seen as well.
Clearer Visibility in Ancient Times?
Schaefer takes pains to emphasize his belief that the age and lag are poor measures of the likelihood a lunar crescent will be visible. These have historically been the main criteria for judging if a crescent could be seen. In the Summary of the above paper he states:
The age and moonset-lag criteria are found to be poor, the altitude/azimuth criteria can make a confident prediction only one-quarter of the time, while the best predictor by far is the modern theoretical algorithm.
The “modern theoretical algorithm” is actually the approach Schaefer himself devised for judging the visibility of a thin lunar crescent, so he has a bias towards it, even if seemingly well-deserved. It should thus not surprise us that he disparages, for one reason or another, earlier attempts using other criteria. But it must be pointed out that a key reason his algorithm works better than other approaches is because it takes atmospheric extinction coefficients for air transparency into account, calculating them “from seasonal, latitudinal and elevation correlations corrected for the seasonal average evening relative humidity” (p. 767). He is thus using current, not ancient, data to develop a theory useful for contemporary crescent predictions.
The interest here, however, is not in modern crescent visibility predictions, but in historical observations and their calendrical implications. Such dates were determined by the ancients using naked-eye sightings during the pre-industrial age, when it may reasonably be argued that the atmosphere on average was more transparent than today, enabling observation of crescent moons at a younger age. Just as we cannot legitimately assume that atmospheric transparency today is the same at all places, elevations and seasons, we cannot assume that at a single location it was the same in ancient times as in ours. The unknown ancient environment at Jerusalem can perhaps be approximated by using higher-elevation locations for sightings; this is reflected in Schaefer’s suggestion that Mauna Kea be used in an attempt to break the earliest unassisted crescent observation record. Commenting on James Stamm’s 12.1 hr telescope-assisted early crescent record, he suggests that
an observer at high altitude in northern California or Nevada should have been able to see Stamm’s record-breaking Moon with the unaided eye. An optimal latitude (such that the Moon stands directly above the Sun) will improve visibility, as will a site with low humidity. For site selection, however, observers should strive for elevation to get above the low-lying atmospheric aerosols. Elevation can make or break a sighting attempt.
Schaefer’s calculations take the expected clarity of the atmosphere – the extinction coefficient – into account, making it a marked improvement over older approaches to estimating when the earliest lunar crescent could be seen. It must be pointed out, though, that all of his data is since the Industrial Revolution. We can expect that in ancient times, except when impacted by volcanic eruptions, lower concentrations of greenhouse gases and cooler average temperatures (with a less dense atmosphere) resulted in the atmosphere being clearer than today. There would thus have been a higher likelihood in the biblical period that the light of a crescent moon could be more fully transmitted and less scattered (less reddened at sunset), particularly during the spring when the air was cooler, less dense, and humidity would have been lower. These factors would logically facilitate the sighting of a thin lunar crescent at a younger age, especially when coupled with the elevation of the Judean highlands. In short, if theory allows for such an early unaided sighting as Stamm’s in our time, we have to wonder what might have been possible for experienced and motivated observers 2000 years ago, in the clear air of early spring in Jerusalem at an elevation of ~2550 feet (780 meters).
In an older paper, “Visibility of the Lunar Crescent” (Q. Jl. Astr. Soc 29 [1988], 511–523), Schaefer compiled 201 lunar sighting reports and used them to analyze his theoretical model for lunar visibility. The ones of interest to us are those where the moon was observed with the unaided eye and its age was ≤18.7 hours. Besides the since-discredited 15.4 hr entry from Schmidt (Schaefer’s entry 44), it also lists naked-eye sightings at 16.5, 16.7 and 17.3 hr, with corresponding lag values of 22, 35, 37 and 38 minutes. With Stellarium giving us an age of 18.7 hr with moonset-lag 40, notwithstanding Schaefer’s low regard for these two criteria, they put an observed crescent on March 20, 6 BC in the realm of possibility.
None of these entries have an ARCL (elongation) as low as the 8.0° value returned by Stellarium. In this regard, in “First Visibility of the Lunar Crescent: Beyond Danjon’s Limit” (The Observatory 127:1 [February 2007], 53–59, online at https://www.astronomycenter.net/pdf/sultan_2007.pdf), A. H. Sultan stated that “an elongation of about 7.5° is the lowest naked eye visibility limit,” though some researchers would push this lower (7° for Danjon and Schaefer, 6.4° for Odeh, 5° for McNally). These comments give theoretical justification for an observation with the 8.0° elongation reported by Stellarium.
The ancient criteria of age and moonset-lag, when coupled with the elongation, thus appear to offer value in evaluating crescent data in a narrow geographical region. Schaefer writes that the “zones of uncertainty” of the ancient criteria encompassed the entire world (Doggett and Schaefer 1994: 399), but we are only interested in comparing data over time from Babylon and Jerusalem. This means we need not concern ourselves with theory built in part on accommodating air transparency, humidity, etc. at other locations. M. Ilyas, who came up with the concept of using a Lunar Date Line (LDL) as a tool for estimating the time of earliest crescent visibility, admitted that “the simple criterion [moonset-lag] is remarkably good for the latitude region where the Ancients [meaning the Babylonians in particular] collected their observational data, illustrating the care with which their data was gathered” (“The Ancients’ Criterion of Earliest Visibility of the Lunar Crescent: How Good is It?” at https://www.cambridgeorg/core/journals/international-astronomical-union-colloquium/article/ancients-criterion-of-earliest-visibility-of-the-lunar-crescent-how-good-is-it/5D6FDE3F000DDFFD6300C805244763ED). Ilyas puts the moonset-lag lunar visibility confidence time at 46 +/- 2 minutes for 30° N latitude (p. 149), slightly more than the 40 minute lag given by Stellarium for Jerusalem at 31.7° N.
Information from Yallop
In 1997, UK astronomer Bernard D. Yallop followed up on Schaefer’s earlier work with his paper, “A Method for Predicting the First Sighting of the New Crescent Moon” (NAO Technical Note No 69, online at https://www.astronomycenter.net/pdf/yallop_1997.pdf). Using the q parameter he devised, he considered 295 pieces of crescent moon sighting data accumulated from 1859 to 1996. He arrived at some different conclusions about crescent visibility (the BDY column in his Table 4) than Schaefer (the BES column).
Unfortunately, his latitude/longitude entries indicate none of his data was obtained from Israel, so the relatively high elevation and specific environmental factors there (humidity and season of the year in particular) cannot be weighed in evaluating Yallop’s data. That said, I regard it as a reasonable, though unprovable, assumption that in the pre-industrial age, the atmospheric extinction coefficient that plays a major role in Schaefer’s, and indirectly Yallop’s, work was generally smaller than in modern times. This would have resulted in clearer air with less light scattering from aerosols and particulate matter, hence improved visibility of younger crescents than is possible today. With this in mind I focused on the crescent records which Yallop regarded as either easily visible (his criterion A), visible under perfect conditions (B), or possibly needing an optical aid to find the crescent (C). I gave less attention to his criterion D (definitely needing an optical aid), and ignored entirely his criteria E and F, where his formula indicated the crescent was not visible. Here is Yallop’s Table 5 explaining his criteria:

In Yallop’s Table 4, some entries he regarded as potentially visible crescents – having visibility codes V(V) or V(F) – are close to most of Stellarium’s March 20, 6 BC values (age 18.7 hr, lag 40, ARCV 7.9°, DAZ 2.4°). They are highlighted in the edited table below. Although there is not a single ARCL value in his A–C classes less than 9.1°, and the lowest given in class D – needing an optical aid to see the crescent – is 8.5°, recall Sultan’s opinion that “an elongation of about 7.5° is the lowest naked eye visibility limit,” while others felt it went as low as 5°. Hence, Stellarium’s 8.0° value should still be regarded as in potentially visible range, just not reflected in the specific data Yallop considered. Also, the ARCL would seem to be the value most directly affected by the atmospheric extinction coefficient; the smaller that angle (DAZ approaching 0°), the less separation of the crescent from the sun and its most intense glare. Clearer air would reduce diffused glare after the sun went below the horizon, increasing crescent visibility.
Yallop also included the following explanatory codes for the columns in Table 4. Particularly important data has been highlighted.
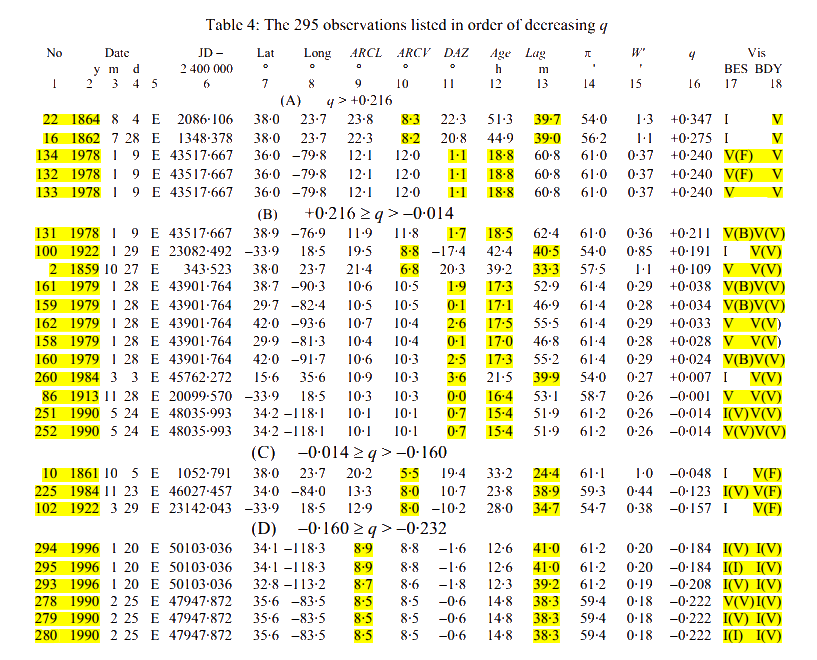
My impression is that Yallop’s ARCL values where q ≤ -0.160 still leave the door open for the crescent moon of March 20, 6 BC being visible. Being ignorant of the atmospheric clarity of Jerusalem in biblical times, we cannot know whether a visual sighting theoretically possible today by first locating the crescent with an optical aid – V(F) – could have been made in ancient times without one by practiced Jewish eyes. Except for the ARCL, the other categories examined – age, lag, ARCV and DAZ – for March 20, 6 BC were all found to imply potential crescent visibility by Yallop.
Hoffman’s LunaCal Program
In addition, the program LunaCal 5.0.1.0 by Roy Hoffman of the Israeli New Moon Society (downloadable at https://moonsocil.blogspot.com/p/lunacal.html) was looked at. A tool for judging the visibility of a young crescent moon, it was used to evaluate Molnar’s determination that March 20, 6 BC was the date of Christ’s birth. Under the default “DALT-width” criterion, LunaCal returns this result: “The New Moon is impossible to see with the naked eye but may be visible with a telescope or with binoculars. The closest to visibility is at 18:31 [6:31 pm].” However, if the Karaite criterion is used for seeing the moon, LunaCal returns, “The New Moon appears on Saturday, 20th March 6 between 18:01 and 18:35 [6:01–6:35 pm] if it is not cloudy. It is very difficult to see, ease of visibility 0.3. Probability of visibility: 30% probability of testimony: 65%.” The Maimonides criterion similarly returns, “The New Moon appears on Saturday, 20th March 6 between 18:01 and 18:35 if it is not cloudy. It is very difficult to see, ease of visibility 0.3. Probability of visibility: 32% probability of testimony: 66%.” Since testimony was important to the ancient Sanhedrin, that 65-66% probability should be noted. For the next day, March 21, 6 BC, LunaCal returns, “The New Moon appears on Sunday, 21st March 6 between 17:52 and 18:38 and fades or sets between 19:02 and 19:42 if it is not cloudy. It is very easy to see, ease of visibility 1.9. Probability of visibility: 100.00% probability of testimony: 100.00%” (emphasis added). All other criteria for seeing the moon that day yield essentially 100% visibility.
I point out here two things. One is that Hoffman’s program predicts that a visible lunar crescent on March 20 was possible using the Karaite criteria, and that 65-66% of observers would be expected to testify they saw the crescent; the second is that just after sunset the next day, March 21, it was a virtual certainty that the crescent was seen, and seen “easily.” This is consistent with the data from Stellarium for March 21, which gives the moon’s age as 40.8 hours at sunset with lag of 95 minutes. If it was seen “easily” that day, this implies it was visible the evening before as well, even if with difficulty.
Lastly, the opinion of the highly-regarded biblical chronologist Jack Finegan can also be noted: he places Nisan 1 in 6 BC on March 20 (Handbook of Biblical Chronology, Table 145, p. 299).
Conclusions
Due to setting aside the CGSF Hebrew calendar in favor of the Exodus Hebrew Calendar as the basis for dating, a re-evaluation of the Priestly Divisions calendar that undergirds the study of the date of Christ’s birth was necessary. It was found that not only did the different intercalation pattern of the Exodus Hebrew Calendar change none of the Hebrew dates essential to the “Pinpointing the Date of Christ’s Birth” study, by moving the date of the start of Jehoiarib’s Temple service from Av 9 to Av 8, a perfect correspondence was achieved with the Seder ‘Olam Rabbah records.
In addition, unlike the CGSF calendar, the Exodus Hebrew Calendar does not identify Nisan 1 with the Saturday Sabbath in 6 BC. Instead it aligns Nisan 1 with Sunday, the first day of the Jewish week. That is a better outcome, because Exodus 40 indicates work (Heb. mela'kah) was being done to construct the Tabernacle all the way up to the time the Shekinah overshadowed it. Since all work was forbidden on the Sabbath, the Exodus Hebrew Calendar works out better than the CGSF calendar by this criterion.
The work of several investigators indicates that a thin crescent sighting on March 20, 6 BC falls within the realm of possibility. In particular, the fact that John Pierce saw with unaided eyes a 15.0 hr crescent with age, lag, ARCL, ARCV and DAZ comparable with the March 20, 6 BC crescent is very significant. Since the intercalation pattern of the Exodus Hebrew Calendar does not allow for a second Adar in 6 BC, Adar only had 29 days that year, requiring Nisan 1 to be pegged to March 21 instead of March 22. The virtual certainty of a crescent sighting the evening of March 21 (lag 95) also justifies the expectation that the crescent was visible, though with difficulty, the previous evening.
In summary, the Exodus Hebrew Calendar is shown to not only offer no conflict with the work already done on the date of Christ’s birth, in several ways it supports it better than the CGSF Hebrew dates originally used. All of these considerations support putting Molnar’s occultation of Jupiter, which he persuasively demonstrated was understood by the Magi as indicating the birth of a King of the Jews, just after sunset on March 20 – the start of Nisan 1. While it must be admitted that the probability of a visual sighting of the crescent the evening of March 20, 6 BC is not favorable by today's criteria, we may presume that ancient Jewish observers, like today’s Karaites, would have been motivated to look very carefully for that crescent moon, particularly because it marked the start of their year. The necessity of 6 BC to not include an Adar-II, to conform with the expected 19-year intercalation pattern, strikes me as the decisive factor.












